ทำความเข้าใจฝุ่น PM 2.5 ในมุมมอง Data Expert
- CORALINE CO. LTD

- 1 ต.ค. 2562
- ยาว 4 นาที
อัปเดตเมื่อ 3 เม.ย. 2566

จากเหตุการณ์ปริมาณ PM2.5 สูงเกินกว่าค่ามาตรฐานที่เรากำลังเผชิญอยู่นั้น เกิดเป็นแรงบันดาลใจให้ทีมงาน Coraline ซึ่งเป็นผู้เชี่ยวชาญด้าน Data Analytics นำข้อมูลต่างๆ มาหาความสัมพันธ์ เพื่อประเมินสาเหตุ และความเกี่ยวข้องต่าง ๆ ที่ก่อให้เกิดฝุ่น PM2.5
ทั้งนี้ ความเข้าใจพื้นฐานของเราทุกคน เชื่อว่า ฝุ่นจะมากับฤดูหนาว ซึ่งความจริงแล้ว อุณหภูมิของอากาศอาจจะเป็นเพียงปัจจัยหนึ่ง และยังมีอีกหลายปัจจัยที่เกี่ยวข้อง เพราะถ้ามีแค่เรื่องของอุณหภูมิ แล้วทำไมแต่ละพื้นที่ ที่มีอุณหภูมิเท่ากัน ถึงมีปริมาณฝุ่นที่แตกต่างกัน
การวิเคราะห์ทางคณิตศาสตร์สามารถตรวจสอบหาความสัมพันธ์ของปัจจัยต่าง ๆ ได้ โดยมีขั้นตอนดังต่อไปนี้
การรวบรวมข้อมูลจากแหล่งข้อมูลต่าง ๆ หรือ Data Collection
การวิเคราะห์ลักษณะของข้อมูล หรือ Exploratory Data Analysis
การสร้าง Model เพื่อพยากรณ์การเกิด PM2.5
การประเมินผลลัพธ์ที่ได้จาก Model หรือ Evaluation
สรุปผล
ในบทความนี้ มีเป้าหมายเพื่อแสดงให้เห็นถึงประโยชน์ของการวิเคราะห์เชิงลึก และการสร้างโมเดลทางคณิตศาสตร์ โดยมีกลุ่มเป้าหมายผู้อ่านเป็นบุคคลทั่วไป ดังนั้นในการนำเสนอ จะมีทั้งในเชิงเทคนิคของการวิเคราะห์ และอธิบายเป็นภาษาที่บุคคลทั่วไปเข้าถึงได้ ทั้งนี้ สำหรับศัพท์เทคนิคบางคำ ทางคณะผู้เขียนบทความ จะขอใช้เป็นคำพิเศษภาษาอังกฤษ ซึ่งจะมีการอธิบายเป็นคำแปลภาษาไทยให้ในครั้งแรกที่มีการกล่าวถึงคำนั้น ๆ
1. Data Collection (การรวบรวมข้อมูล)
ข้อมูลที่ใช้วิเคราะห์ มาจากแหล่งข้อมูลที่เปิดเผยสู่สาธารณะโดยทั้งสิ้น ได้แก่
ข้อมูล PM2.5: http://berkeleyearth.lbl.gov/air-quality/local/Thailand/Bangkok
ข้อมูลสภาพอากาศ: https://www.wunderground.com/history/daily/th/bangkok
ข้อมูลดัชนีการจราจร: http://traffic.longdo.com
2. Exploratory Data Analysis (การวิเคราะห์ลักษณะของข้อมูล)
- ข้อมูลของ PM2.5 เป็นข้อมูลการวัดค่าความหนาแน่นของฝุ่น PM2.5 ในหน่วย (µg/m3 )เฉลี่ยรายชั่วโมง ซึ่งข้อมูลที่นำมาใช้นั้น เป็นข้อมูลที่อยู่ภายในพื้นที่กรุงเทพมหานคร โดยมีตัวอย่างของข้อมูลดังนี้

- สร้างกราฟเพื่อดูลักษณะการเกิด PM2.5 ในแต่ละช่วงเวลา โดยให้แกน X เป็นช่วงเวลาในแต่ละวัน และแกน y เป็น ปริมาณ PM2.5 เฉลี่ยในช่วงเวลานั้น สีของกราฟแทนวันที่แต่ละวันในเดือนมกราคม ปี 2019

ภาพที่ 1: แสดงปริมาณฝุ่น PM2.5 ในช่วงเวลา 0.00 น.-24.00น. ระหว่างวันที่ 8-15 มกราคม 2019

ภาพที่ 2: แสดงปริมาณฝุ่น PM2.5 ในช่วงเวลา 0.00 น.-24.00น. ระหว่างวันที่ 15-22 มกราคม 2019

ภาพที่ 3: แสดงปริมาณฝุ่น PM2.5 ในช่วงเวลา 0.00 น.-24.00น. ระหว่างวันที่ 22-28 มกราคม 2019
- จากกราฟจะพบว่า ลักษณะการเกิดฝุ่นในแต่ละช่วงเวลามีแนวโน้มใกล้เคียงกัน โดยปริมาณฝุ่นจะมีค่าต่ำสุดในช่วงเวลาระหว่าง 10.00 น. จนถึง 15.00 น. และจะค่อย ๆ เพิ่มขึ้นเรื่อย ๆ จนสูงสุดในช่วง 02.00 น. จนถึง 03.00 น.
- จากสมมติฐานเบื้องต้น จึงได้มีการหาปัจจัยอื่น ๆ เพิ่มเติมในการหาความสัมพันธ์กับปริมาณฝุ่น โดยมีปัจจัยที่นำมาเปรียบเทียบดังนี้
Temperature: อุณหภูมิ หน่วยเป็นฟาเรนไฮน์
Dew Point: จุดไอน้ำกลั่นตัว หน่วยเป็นองศาฟาเรนไฮ
Humidity: ความชื้น หน่วยเป็น %
Wind Speed: ความเร็วลม หน่วยเป็น mile per hour
และเมื่อนำข้อมูลจากแต่ละปัจจัยมาสร้างกราฟเพื่อเปรียบเทียบกับปริมาณฝุ่น PM2.5 ในแต่ละช่วงเวลา จะได้กราฟดังนี้

ภาพที่ 4: แสดงปริมาณฝุ่น PM2.5 ความเร็วลม อุณหภูมิ ความชื้น และจุดไอน้ำกลั่นตัว
- จากกราฟในภาพที่ 4 จะพบว่า มีปัจจัยบางอย่างที่มีลักษณะแสดงเป็นความสัมพันธ์กับปริมาณฝุ่น ได้แก่
Wind Speed: ในช่วงที่ Wind Speed สูง ปริมาณของ PM2.5 จะลดลง
Temperature: ในช่วงที่อุณหภูมิสูง ปริมาณของ PM2.5 จะลดน้อยลง
โดยจะสามารถวิเคราะห์ความสัมพันธ์ระหว่างปัจจัยต่าง ๆ ได้โดย 2 วิธีดังนี้
2.1 Scatter Plot
การเปรียบเทียบระหว่างปัจจัยต่างๆ กับปริมาณ PM2.5 ซึ่งสามารถเปรียบเทียบเบื้องต้นโดยการสร้างกราฟ Scatter Plot จากข้อมูลย้อนหลัง
อุณหภูมิ:
จากภาพที่ 5 พบว่า ในช่วงอุณหภูมิต่ำ ระหว่าง 15-20 ℃ มีแนวโน้มของ PM2.5 ในปริมาณที่ต่ำ แต่ปริมาณของชุดข้อมูลที่มีช่วงอุณหภูมิดังกล่าว ก็มีน้อยด้วยเช่นกัน เป็นเพราะช่วงเวลาที่กรุงเทพมีอุณหภูมิต่ำนั้นเกิดขึ้นน้อยนั่นเอง
ในช่วงที่อุณหภูมิมีค่าระหว่าง 21-34 ℃ เป็นช่วงที่ปริมาณ PM2.5 มีแนวโน้มสูง ก่อนที่จะเริ่มลดลงมาในช่วงอุณหภูมิ 35-40 ℃
แนวโน้มความสัมพันธ์ของอุณหภูมิและปริมาณ PM2.5 นั้นไม่แน่ชัด

ภาพที่ 5: แสดงกราฟ Scatter Plot เปรียบเทียบระหว่างปริมาณ PM2.5 และอุณหภูมิ
ความเร็วลม:
จากภาพที่ 6 พบว่าแนวโน้มของปริมาณ PM2.5 จะมีค่าสูง เมื่อความเร็วลมมีค่าน้อย และเมื่อความเร็วลมมีค่าสูงขึ้น ปริมาณ PM2.5 จะมีแนวโน้มที่ลดลง

ภาพที่ 6: แสดงกราฟ Scatter Plot เปรียบเทียบระหว่างปริมาณ PM2.5 และความเร็วลม
เดือน:
จากภาพที่ 7 จะเห็นว่าแนวโน้มค่าสูงสุดของปริมาณ PM2.5 จะมีค่าสูงในช่วงเดือนมกราคมถึงเดือนมีนาคม ก่อนที่จะเริ่มลดลงในเดือนเมษายน และมีค่าน้อยในช่วงเดือนพฤษภาคมจนถึงเดือนกันยายน ก่อนที่จะกลับขึ้นสูงอีกครั้งในเดือนตุลาคมจนถึงเดือนธันวาคม
อย่างไรก็ตามแนวโน้มของค่าต่ำสุดของปริมาณของ PM2.5 ในแต่ละเดือนนั้นไม่มีความแตกต่างกันอย่างมีนัยสำคัญ

ภาพที่ 7: แสดงกราฟ Scatter Plot เปรียบเทียบปริมาณ PM2.5 ในเดือนต่างๆ
ความชื้นสัมพัทธ์:
จากภาพที่ 8 พบว่าแนวโน้ม PM2.5 ในปริมาณที่สูงนั้น มีการกระจายอยู่เกือบทุกช่วงของความชื้น
ข้อสังเกตคือช่วงที่ความชื้นสัมพัทธ์มีค่าน้อยกว่า 40% แนวโน้มของปริมาณฝุ่น PM2.5 มีค่าน้อย และช่วงที่มีความชื้นสัมพัทธ์ 100% ก็มีแนวโน้มของปริมาณฝุ่นน้อยเช่นเดียวกัน
แนวโน้มความสัมพันธ์ของความชื้นสัมพัทธ์และปริมาณ PM2.5 นั้นไม่แน่ชัด
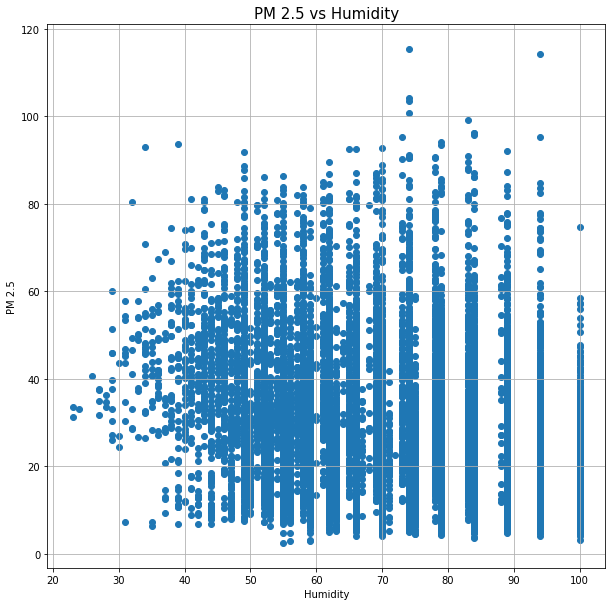
ภาพที่ 8: แสดงกราฟ Scatter Plot เปรียบเทียบระหว่างปริมาณ PM2.5 และความชื้
การจราจร:
จากภาพที่ 9 จะเห็นว่าแนวโน้ม PM2.5 ในปริมาณที่สูงนั้น มีการกระจายอยู่แทบทุกช่วงของค่าดัชนีการจราจร รวมไปถึงช่วงที่มีค่าดัชนีการจราจร ระหว่าง 0-2 ในทางกลับกันในช่วงที่มีค่าดัชนีการจราจรที่สูง ระหว่าง 8-10 กลับมีแนวโน้มของปริมาณ PM2.5 สูง ที่น้อยกว่าช่วงอื่นๆ ดังนั้นดัชนีการจราจรไม่มีความสัมพันธ์ต่อปริมาณ PM2.5

ภาพที่ 9: แสดงกราฟ Scatter Plot เปรียบเทียบระหว่างปริมาณ PM2.5 และความหนาแน่นของการจราจร
จุดไอน้ำกลั่นตัว:
จากภาพที่ 10 จะเห็นว่าเมื่อจุดไอน้ำกลั่นตัวมีค่าระหว่าง 60-73 F ปริมาณฝุ่น PM2.5 สูงสุดมีแนวโน้มเพิ่มขึ้น จากนั้นจึงกลับมามีแนวโน้มลดลงตั้งแต่ช่วง 75 F เป็นต้นไป โดยสังเกตว่าในช่วงที่จุดไอน้ำกลั่นตัวมีค่าน้อยกว่า 59 F มีปริมาณข้อมูลน้อยกว่าช่วงอื่นๆ
แนวโน้มความสัมพันธ์ของจุดไอน้ำกลั่นตัว และปริมาณ PM2.5 นั้นไม่แน่ชัด

ภาพที่ 10: แสดง Graph Scatter Plot เปรียบเทียบระหว่างปริมาณ PM2.5 และจุดไอน้ำกลั่นตัว
2.2 Correlation
การวิเคราะห์ความสัมพันธ์ระหว่างตัวแปร 2 ตัว โดยใช้ Correlation เป็นการอธิบายว่าตัวแปรแต่ละตัวที่นำมาเปรียบเทียบกันนั้น มีแนวโน้มไปในทิศทางเดียวกัน หรือ ตรงข้ามกันอย่างมีนัยสำคัญหรือไม่
Correlation จะมีค่าอยู่ระหว่าง -1 และ 1 โดยสามารถแบ่งการตีความได้เป็น 2 ส่วน
1. เครื่องหมาย:
a. ในกรณีที่ Correlation มีค่าติดลบ หรือมีค่าน้อยกว่า 0 หมายถึง ตัวแปรทั้ง 2 ตัวนั้นมีค่าความสัมพันธ์ที่ผกผันกัน
b. ในกรณีที่ Correlation มีค่ามากกว่า 0 หมายถึงตัวแปรทั้ง 2 ตัว มีความสัมพันธ์ไปในทิศทางเดียวกัน
2. ขนาด:
a. ในกรณีที่ขนาดของ Correlation มีค่าเข้าใกล้ 1 หมายถึง ตัวแปรทั้ง 2 ตัวมีความสัมพันธ์ในเชิงเส้นตรงกันมาก
b. ในกรณีที่ขนาดของ Correlation มีค่าเข้าใกล้ 0 หมายถึง ตัวแปรทั้ง 2 ตัว ไม่มีความสัมพันธ์เชิงเส้นตรงกัน
โดยเมื่อนำข้อมูลในช่วงระหว่างเดือน มีนาคม 2016 - มกราคม 2019 มาสร้างตาราง Correlation จะได้ผลดังแสดงในภาพที่ 11

ภาพที่ 11: แสดง Correlation ระหว่างปริมาณ PM2.5 และปัจจัยอื่นๆ
จากภาพที่ 11 จะเห็นว่าปัจจัยที่มีแนวโน้มไปในทางเดียวกัน และมีค่าสัมพันธ์เชิงเส้นตรงกับปริมาณฝุ่น PM2.5 ที่สุดคือ ความดัน และปัจจัยที่มีแนวโน้มผกผัน และมีความสัมพันธ์เชิงเส้นตรงกับปริมาณฝุ่น PM2.5 มากที่สุดคือจุดไอน้ำกลั่นตัว รองลงมาคือความชื้นสัมพัทธ์ ความเร็วลม และเดือน ตามลำดับส่วนปัจจัยที่มีความสัมพันธ์เชิงเส้นตรงกับปริมาณฝุ่นน้อยได้แต่ อุณหภูมิ ดัชนีการจราจร เวลาในแต่ละวัน และวันในแต่ละสัปดาห์
จากการตรวจสอบความสัมพันธ์จาก Scatter Plot และ Correlation แล้วในลำดับถัดไปจะเป็นการคาดการณ์ปริมาณฝุ่น PM2.5 โดยใช้ Machine Learning Model เพื่อพยากรณ์การเกิด PM2.5
3. Forecasting Model หรือ การสร้าง Model เพื่อพยากรณ์การเกิด PM2.5
การสร้าง Forecasting Model ตามหลักของ Data Science จะมี 2 วิธี คือ Time-Series Model กับ Regression Model ซึ่งต่างกันตรงที่ Time-Series Model จะใช้ตัวเองในอดีต มาทำนายตัวเองในอนาคต ในขณะที่ Regression Model จะสามารถใช้ปัจจัยอื่น ๆ ที่เกี่ยวข้องเป็นส่วนประกอบของการทำ Model ได้
Model ที่ทาง Coraline เลือกใช้ คือ Regression Model เนื่องจากเราต้องการศึกษาปัจจัยต่าง ๆ ที่ส่งผลต่อปริมาณของ PM2.5
การสร้าง Regression Model จะมีการแบ่งข้อมูลออกเป็น 2 ชุด ได้แก่ Training Data เพื่อเป็นต้นแบบในการสร้าง Model ในชุดข้อมูล ประกอบไปด้วย Feature หรือปัจจัยที่ส่งผลให้เกิด PM2.5 และ Target หรือ ตัวแปรที่เราต้องการทำนาย ในที่นี้ คือ ปริมาณ PM2.5 และส่วนของ Testing Data จะเป็นชุดข้อมูลในลักษณะเดียวกัน แต่มิได้นำข้อมูลส่วนนี้ไปสร้าง Model เพราะต้องการเก็บข้อมูลชุดนี้ เพื่อทดสอบความถูกต้องของ Model นั่นเอง
Feature หรือ ปัจจัยต่าง ๆ ใช้ในการสร้าง Model ประกอบไปด้วย
Temperature: อุณหภูมิ (F)
Dewpoint: จุดไอน้ำกลั่นตัว (F)
Humidity: ความชื้นสัมพัทธ์ (%)
Windspeed: ความเร็วลม (mph)
Pressure: ความดัน (inches of mercury)
Condition: สภาพอากาศ (Fog/Fair/Partly Cloudy)
Year: ปีคริสตศักราช
Hour: เวลาในแต่ละวัน (0.00-24.00)
Month: เดือนในแต่ละปี (1-12)
Day of Week: วันในสัปดาห์ (Mon-Sun)
PM2.5 Last week: ปริมาณ PM2.5 ณ ช่วงเวลาเดียวกันของสัปดาห์ก่อน (µg/m3)
PM2.5 last week: ปริมาณ PM2.5 ณ ช่วงเวลาเดียวกันของปีก่อน (µg/m3)
Target หรือ เป้าหมาย คือ PM2.5 Next Week: ปริมาณ PM2.5 ณ สัปดาห์ถัดไป
เหตุผลที่ทีม Coraline เลือกใช้ PM2.5 ในสัปดาห์ถัดไปเป็น Target ก็เพื่อให้เกิดระยะห่างเพื่อสามารถนำผลลัพธ์ไปใช้ได้จริงในเชิงการเตรียมตัว และบริหารจัดการ ซึ่งในทางทฤษฎีแล้ว การพยากรณ์ที่มีช่วงระยะเวลาห่างนั้น ยิ่งหาก จะยิ่งมีโอกาสที่ผลลัพธ์จะแม่นยำได้น้อยกว่า ในขณะเดียวกัน ทางทีมมองว่า หากพยากรณ์ในช่วงเวลากระชั้นชิด ก็อาจจะไม่สามารถเตรียมตัว หรือบริหารจัดการได้ทัน เช่น การพยากรณ์ล่วงหน้า 1 ชั่วโมง แม้จะมีความแม่นยำสูง การทำนายล่วงหน้าที่ใกล้จนเกิดไปก็อาจไม่เกิดประโยชน์ใด
Training Set Period: 1 มกราคม 2017 - 10 มกราคม 2019
Testing Data
Test Set Period: 11-17 มกราคม 2019
Model
GradientBoostingRegressor
Model Machine Learning ประเภท Regression จาก Library Sci-Kit Learn
มีรูปแบบเป็น Tree Regressor Model
Parameter Setup: Boosting Stage to Perform (n estimator) = 300
4. Evaluation หรือ การประเมินผลลัพธ์ที่ได้จาก Model
หลังจากได้ Model เพื่อพยากรณ์ปริมาณฝุ่น PM2.5 โดยใช้ Model แล้วนั้น ในลำดับต่อมา คือ การประเมินผลลัพธ์ที่ได้จาก Model โดยสามารถแบ่งการวัดผลออกเป็น 2 แบบ
Scale independent: ผลของค่าที่ได้จะมีหน่วยเดียวกับ Target
a. Root Mean Square Error: เป็นการวัด Error โดยการเทียบค่าที่ได้จากการทำนาย กับค่าที่เกิดขึ้นจริง โดยค่า Error จะเป็นไปดังสมการที่ 1

b. Mean Absolute Error:เป็นการวัด Error โดยการเทียบค่าที่ได้จากการทำนาย กับค่าที่เกิดขึ้นจริง โดยค่า Error จะเป็นไปดังสมการที่ 2

2. Scale Dependent: ผลของค่าที่ได้จะอยู่ในรูปแบบ Percentage
a. R-Square: เป็นค่าที่บอกว่าผลลัพธ์ที่ได้จาก Model เทียบกับค่าจริงแล้ว มีแนวโน้มไปใน ทิศทางเดียวกันมากน้อยเพียงใด
โดยค่า R-Square เป็นไปดังสมการที่ 3
ค่า R-Square มีค่าระหว่าง -1 ถึง 1 โดยยิ่งมีค่าเข้าใกล้ 1 นั่นหมายความว่าผลที่ได้จากการทำนาย และค่าจริงมีทิศทางไปในทางเดียวกัน

b. Symmetric Mean Absolute Percentage Error (SMAPE): เป็นการหาค่า Error โดยมี การนำส่วนต่างค่าที่ได้จาก Model และค่าจริง เทียบกับผลบวกของ ค่าทั้งสองด้วย ทั้งนี้เพื่อลดความผิดพลาดในการตีความในกรณีที่ค่าทั้งสองมีค่าน้อย โดยค่า SMAPE เป็นไปดังสมการที่ 4
ค่า SMAPE มีค่าอยู่ระหว่าง 0-1
เนื่องจากสมการเป็นค่า error ดังนั้นยิ่งมาน้อยยิ่งดี

ผลลัพธ์ที่ได้จากการประเมิน Modelหลังจากการ Train Model โดยใช้ Training Set ตามรายละเอียดในส่วนของ Training Data แล้วจึงใช้ข้อมูลในช่วงของ Testing Data ในการทำนาย และตรวจสอบผล โดยได้ผลลัพธ์ดังนี้

ภาพที่ 12: แสดงผลลัพธ์ที่ได้จากการทำนาย PM2.5 เทียบกับ ปริมาณ PM2.5 ที่เกิดขึ้นจริง
จากผลลัพธ์ที่ได้จึงมีการประเมินผลลัพธ์ โดยใช้ค่าต่างๆ ดังต่อไปนี้
Root Mean Square Error (RMSE): 15.465 µg/m3
Mean Absolute Error (MAE): 12.492 µg/m3
R-Square: -0.152
Symmetric Mean Absolute Percentage Error (SMAPE): 27.72 %
5. สรุปผล
แม้ว่าผลที่ได้จะมี Error ที่ค่อนข้างน้อย (ประมาณ 27%) แต่ค่า R-Square นั้นมีค่าติดลบ นั่นหมายถึง แนวโน้มระหว่างปริมาณ PM2.5 ที่เกิดขึ้นจริง กับที่ได้จากการทำนายยังมีแนวโน้มไม่ตรงกัน อาจเป็นเพราะปัจจัยที่อยู่ใน Model อาจจะยังไม่ครบ เช่น ขาดข้อมูล UV Index ข้อมูลการเผาขยะ ข้อมูลไฟป่า เป็นต้น หรือ การเลือกระยะห่างของการพยากรณ์ที่กว้างจนเกินไป
อย่างไรก็ตาม แม้การทดลองนี้ จะไม่ได้แสดงผลลัพธ์ที่แม่นยำมากนัก แต่สิ่งที่ได้เรียนรู้จากการวิเคราะห์ คือ
แต่ละพื้นที่ อาจจะมีต้นเหตุของการเกิดฝุ่น PM2.5 ที่ไม่เหมือนกัน ในการสร้าง Model อาจจำเป็นต้องสร้าง Model ในแต่ละพื้นที่ที่ไม่เหมือนกัน เช่น ในเขตเมือง ที่ราบสูง หรือเขตนอกเมือง เป็นต้น และหากเป็นเช่นนั้น ก็แสดงว่า แนวทางในการแก้ปัญหาฝุ่น PM2.5 ก็ควรมีแนวทางที่แตกต่างกันในแต่ละพื้นที่ด้วยเช่นกัน
ข้อมูลที่นำมาใช้วิเคราะห์ ยังมีปริมาณที่ไม่มากพอ และเป็นข้อมูลในเชิงภาพรวม เช่น อุณหภูมิในกรุงเทพมหานคร มิได้ลงรายละเอียดว่าเป็นบริเวณไหน เป็นบริเวณเดียวกันที่เกิดฝุ่นหรือไม่ เป็นต้น
การพยากรณ์ที่มีระยะห่าง ยิ่งห่างมาก ก็ยิ่งมีความยากในการทำงาน แต่ในทางปฏิบัติ การเตรียมตัวล่วงหน้า จะเกิดประโยชน์ได้มากกว่าการรู้ข้อมูลแบบฉับพลัน ดังนั้นการออกแบบ Model จึงต้องคำนึงถึงการใช้งานเป็นหลัก
การสร้าง Model หรือการทำงานของ Data Scientist มิใช่เพียงการนำข้อมูลไปสร้าง Model แต่เป็นการเตรียมข้อมูล และอธิบายความสัมพันธ์ของข้อมูลก่อนที่จะนำข้อมูลนั้นไปสร้าง Model และประเมินผลลัพธ์ต่อไป
กระบวนการสร้าง Model คือ การลองผิดลองถูก อาจจะต้องทำซ้ำๆ เปลี่ยนชุดข้อมูล เปลี่ยนวิธีการใช้ Algorithm จนกว่าจะเจอ Model ที่เหมาะสม
สุดท้ายนี้ สิ่งที่ทีม Coraline อยากจะถ่ายทอด คือ เรายังขาดข้อมูลที่พร้อมใช้อีกมาก ซึ่งหากเรามีข้อมูลที่ละเอียดขึ้น เป็นข้อมูลที่มีคุณภาพ ก็อาจจะสามารถวิเคราะห์มูลเหตุของการเกิด PM2.5 ได้ลึกขึ้นนำไปสู่การแก้ปัญหาที่ตรงจุด
หลายครั้งที่มีคนถามว่า โครงการ Big Data ทำไปเพื่ออะไร คำตอบก็คือ เพื่อเราจะได้มีแนวทางในการตัดสินใจที่ชัดเจนขึ้น โดยใช้ Big Data เป็นทรัพยากรในการวิเคราะห์ หาทางเลือก เสนอเป็นทางออก แต่ถ้าไม่มีทรัพยากรเลย ก็ยากที่จะมี “หลักฐาน” หรือ “แนวทาง” ใดๆเกิดขึ้น
ทั้งนี้ การจะมี Big Data ได้นั้น มีหลายองค์ประกอบ ทั้งแหล่งที่มาของข้อมูล ที่อาจจะต้องเป็นอุปกรณ์ หรือ ระบบเก็บข้อมูล การเชื่อมโยงข้อมูลที่เหมาะสม Data Storage หรือ ที่เก็บข้อมูลที่มีประสิทธิภาพที่ดี ทำให้สามารถนำเข้า และส่งต่อข้อมูลได้อย่างรวดเร็ว
สิ่งที่เป็นอุปสรรค์สำหรับโครงการ Big Data ก็คือ ยังไม่เห็นประโยชน์ และยังไม่รู้ว่าจะใช้ Data ไปทำอะไร เพื่ออะไร เรื่องราวเกี่ยวกับฝุ่น PM 2.5 ในมุมมอง Data Expert ในวันนี้ จะเป็นอีกตัวอย่างหนึ่ง ที่แสดงให้เห็นว่า การไม่มีทรัพยากรที่ดี (ในที่นี้ คือ Data) ก็อาจจะเป็นสาเหตุหนึ่ง ที่ทำให้เรายังไม่มีการวิเคราะห์ที่ถูกสุด จนกระทั่งยังไม่สามารถมองหาแนวทางในการแก้ปัญหาที่เกิดขึ้นได้
PM2.5 จะมาอีกกี่ปี เราคงไม่สามารถพยากรณ์ได้ หวังเพียงว่าในแต่ละปี เราจะได้เห็นการพัฒนาอะไรบางอย่าง เพื่อลดภัยร้ายจากฝุ่น PM2.5 นี้ เพราะเรื่องสุขภาพอนามัย เป็นเรื่องใกล้ตัวของเราทุกคน












Comments